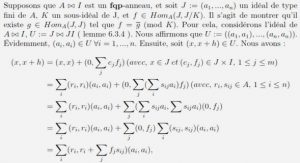INTRODUCTION
En 1972, Kowalski a étudié dans [KOW72] l’existence d’une structure riemannienne pour une connexion linéaire, sans torsion, à courbure régulière. Il a trouvé à cet effet quelques résultats tels que la détermination d’une métrique riemannienne régulière par le tenseur de courbure et aussi des conditions nécessaires et suffisantes pour qu’une connexion linéaire sans torsion sur une variété de dimension n, n ≥ 2, soit une connexion de LeviCivita. Dans cette même optique, J. Vey a étudié une connexion linéaire sans torsion pour qu’elle soit de Levi-Civita, dans un papier non publié. Dans ce présent mémoire, nous adoptons un point de vue plus général : le cadre le plus approprié est la variété finslerienne et que les connexions ne sont pas forcément linéaires. En d’autres termes, nous établissons des conditions nécessaires et suffisantes pour qu’une connexion sans torsion, à courbure régulière, provienne d’une structure finslerienne. Le formalisme de Grifone [GRI72] est en effet un outil de base dans ce travail. Pour se faire, nous étudions en premier lieu les notions fondamentales telles que les formes vectorielles et leur crochet de Frölicher-Nijenhuis, la 1-forme vectorielle J appelée aussi structure tangente naturelle. En second lieu, nous nous approfondissons les concepts de connexions : ce sont des formes vectorielles d’ordre 1 sur l’espace fibré TM de M. Cette connexion définit une structure presque produit sur TM et permet la décomposition de l’espace T TM en deux sous-espaces : le sous-espace horizontal et le sous-espace vertical. Dans cette partie, nos connaissances vont s’élargir sur les notions de courbure et de torsion d’une connexion donnée. Enfin, la dernière partie de cet ouvrage se consacre sur les variétés finsleriennes notamment sur l’existence d’une structure finslerienne de dimension n ≥ 2 à connexion donnée, en particulier pour n = 2. On remarque que cette hypothèse n = 2 nous permet d’avoir une courbure nulle si l’espace de nullité horizontal de la courbure de la connexion est non nul, cf. [RRA15]. Chaque section est accompagnée par des exemples illustratifs. Dans certains exemples, nous utilisons le logiciel de calcul Mathématiques « Maple », version 13, pour effectuer les calculs assez longs et parfois complexes. La convention d’Einstein de sommation sur les indices répétés est systématiquement utilisée.
Le fibré π∗(TM)[DJE01]
Le fibré pull-back (ou fibré rappelé) π∗(TM) −→ T M, dont la base est le fibré tangent privé de la section nulle T M, est décrit comme une collection d’espaces tangents TxM en chaque point (x, y) de la base T M. En effet, la collection de tous les points (x, y) avec y 6= 0, constituant le fibré tangent T M, est considérée comme une variété où en chaque point (x, y) est dressé une copie de TxM sur lequel un produit scalaire peut être formé. L’appellation ”fibré rappelé” pour π∗(TM), issue du langage de la théorie des fibrés, vient du fait qu’il est construit à partir du fibré tangent TM comme suit π∗(TM) = {(x, y, v) ∈ T M × TM : π(x, y) = π(v) = x}, et on a le diagramme
Définition 1.8. [KLE87] Soit M une variété, F = F (M) l’anneau des fonctions C ∞ sur M, X = X (M) le F-module des champs de vecteurs sur M et Λ (M) l’algèbre extérieure sur M. Une l-forme vectorielle L sur M, 0 ≤ l ≤ n, est une application linéaire alternée L : Xl −→ X, c’est-à-dire un tenseur de type (1, l) complètement antisymétrique.
Pour l = 0, L est un champ de vecteurs sur M.
Pour l = 1, on a L : X −→ X, donc L est un endomorphisme de X, et on dit tout simplement une 1-forme vectorielle. Et pour l = 2, on a L : X × X −→ X, L est une application bilinéaire complètement antisymétrique, et ainsi de suite suivant la valeur del. En particulier, la transformation identique I dans X est une 1-forme vectorielle.
Exemple 1.9. Une matrice carrée d’ordre n sur un corps K est une 1-forme vectorielle sur K. Dans toute la suite, le terme « forme » désignera une forme différentielle extérieure. Par contre, les « formes vectorielles » seront toujours précisées avec cette appellation.
CONCLUSION
Ce présent mémoire à pour but l’étude des variétés finsleriennes du point de vue de la connexion de Grifone à courbure non nulle. Nous avons défini une connexion à l’aide de sa gerbe. Cette connexion est à torsion nulle et a la forme Γ = [J, S], où S est la gerbe associée à la connexion et J la structure tangente naturelle sur la variété M. Grace à l’isotropie de la gerbe, la courbure d’une connexion donnée peut se mettre sous la forme 3R = (dJ λ − η) ∧ J + dJ η ⊗ C, où λ ∈ C∞(T M) et η une 1−forme semibasique sur C∞(T M). Cette relation nous permet de simplifier certains calculs dans ce présent travail. En combinant cette dernière formule avec des résultats jugés indispensables, nous arrivons à prouver l’existence d’une structure finslerienne de dimension 2 à connexion donnée ; toute courbure étant bien sûr régulière, d’après M. Matsumoto dans [MAT95]. L’existence d’une fonction énergie E homogène de degré 2, non triviale telle que dRE = 0 peut aussi être prouvée directement à l’aide du théorème de Fröbenius, puisque l’image de la courbure est de dimension 1. Bref, la théorie des connexions finsleriennes a été abordée par plusieurs auteurs suivant des points de vue différents. L’étude qui peut s’étendre à partir de ce travail est de déterminer les notions ainsi que les résultats similaires dans une dimension supérieure stricte à 2, surtout un des théorèmes que nous avons démontré nous le garantit. Le point de vue algébrique sera à cet effet plus maniable et donc passionnant pourquoi pas ?
|
Table des matières
Introduction
1 Préliminaires
1.1 Rappels
1.2 Tenseurs canoniques sur TM
1.2.1 Le fibré π∗(TM)
1.2.2 L’endomorphisme vertical J et le champ canonique C
1.3 Dérivations algébriques
1.4 Formes semi-basiques et formes homogènes
1.5 Semi-gerbes et gerbes
2 Généralités sur les connexions
2.1 Définitions et théorèmes
2.2 Projecteur vertical et Projecteur horizontal
2.3 Semi-gerbe associée à une connexion
2.4 Courbure et torsion d’une connexion
3 Variétés semi-finsleriennes et finsleriennes
3.1 Variétés semi-finsleriennes
3.1.1 Semi-gerbe associée canoniquement à une structure semi-finslerienne
3.1.2 Connexions conservatives
3.2 Variétés finsleriennes
3.2.1 Existence d’une fonction énergie d’une connexion
3.2.2 Existence d’une structure finslerienne de dimension 2 à connexion donnée
Conclusion
Bibliographie
Télécharger le rapport complet