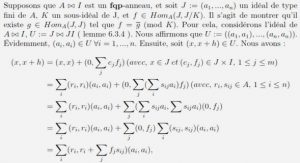Introduction
Le sujet principal de cette thèse est l’étude du comportement spectral des opérateurs de déplacement avec poids et les équations cohomologiques qui leur sont associées.
La théorie des opérateurs de déplacement pondéré, a joué un rôle fondamental dans le développement des mathématiques pures et appliquées. Elle repose sur les espaces fonctionnels ( sur lesquels ces opérateurs sont définis ), considérés en général sur les espaces de Banach.
Ces opérateurs ont fait l’objet d’intenses recherches au cours des dernières décennies et apparaissent dans des domaines variés des mathématiques tels que la physique mathématique, la théorie des équations intégro-fonctionnelles ou intégro-différentielles, la théorie des systèmes dynamiques, la théorie des opérateurs de convolution et bien d’autres.
Les opérateurs de déplacement avec poids ont été étudiés généralement dans les espaces de fonctions continues et dans les espaces LP(X, µ).
L’étude de ces opérateurs a connu un développement accru dans les travaux d’un bon nombre de mathématiciens parmi lesquels on peut citer dans cette direction, les travaux remarquables de [3, 34, 32, 26, 29, 42]. L’un des problèmes d’actualités est l’étude de ces opérateurs dans le cas d’un déplacement quelconque ( pas forcément inversible).
Probablement le premier résultat se rapportant aux opérateurs de déplacement dans un espace quelconque est le théorème de Kamowitz-Scheinberg [24], dans lequel a été prouvé que si l’espace F (X ) est une algèbre commutative semi-simple de Banach et T αun automorphisme non périodique alors, le spectre de l’opérateur T α contient la circonférence unitaire S1.
Spectre d’un opérateur de déplacement
Pour ce qui de la dynamique de l’application α, il nous est nécessaire de formuler certaines définitions. Comme il apparaîtra plus tard, de cette dynamique dépendront les propriétés spectrales de l’opérateur T α.
Opérateurs de composition pondérée sur L 2
L’objet principal de ce chapitre est l’étude des propriétés spectrales des opérateurs de déplacement pondéré définis dans des espaces de fonctions L 2 (X, µ) où µ est la mesure de Lebesgue par.une application donnée de X dans lui même, la fonction a(·) étant donnée, telle que l’opérateur de multiplication par la fonction a conserve l’espace F (X). Si a est la fonction identité, alors l’opérateur A est tout simplement appelé opérateur de composition et, est désigné par
Dans cette optique, nous introduisons la notion d’opérateurs de déplacement pondéré et explicitons le lien entre ses propriétés spectrales et les équations cohomologiques.
Nous énonçons également un théorème donnant une condition suffisante pour qu’une équation cohomologique soit solvable, ou encore soit normalement solvable ; celle-ci repose sur des propriétés spectrales fines de l’opérateur considéré. C’est pourquoi, nous établissons au préalable, des résultats spectraux concernant un shift bilatéral pondéré sur l’espace séparable et de dimension infinie, qui permettent d’appliquer le critère de solvabilité des équations cohomologiques, pour une certaine classe de fonctions ayant exactement deux points fixes ou de points selles.
Opérateurs de la forme T
On considère dans ce sous chapitre, l’opérateur de composition, noté T α sur L 2 (X, µ) défini par les propriétés spectrales des opérateurs de la composition avec poids. Pour certaines classes d’applications, ces propriétés ont été décrites dans les papiers [6, 45, 46].
Pour donner le résultat dans une forme explicite, nous considérerons une sous-classe de telles applications α et ensuite, il nous sera facile d’obtenir une généralisation
Influence des points selles sur les propriétés spectrales
Les applications du segment étudiées plus haut possèdent les propriétés dynamiques les plus simples. Nous notons une classe d’application où chaque trajectoire converge vers un certain point fixe et où le nombre de tels points fixes est fini et de façon beaucoup plus générale, des applications où en plus des points d’attraction ou de répulsion il existe des points fixes d’un autre type c’est à dire les points selles.
Dans les travaux [3, 6] il a été examiné les propriétés spectrales fines d’une classe modèle d’opérateur, engendré par les applications possèdant des points selles. Dans cette section, Comportement spectral des opérateurs de dépalcement avec poids et équation cohomologique MBAINAISSEM Teubé Cyrille c UCAD de Dakar / 2015 Influence des points selles sur les propriétés spectrales 23 nous donnons la description des propriétés spectrales de l’opérateur T α pour une classe des difféomorphismes
Opérateurs de déplacement pondérés réductibles
Le lien entre le problème de la factorisation avec l’équation homologique pour les fonctions ayant des valeurs positives a été montré ci-dessus. Dans le cas de fonctions à valeurs complexes, des complications supplémentaires apparaissent pour obtenir l’équation homologique, difficulté émanant du fait que le logarithme est une fonction multivoque.
Nous dirons qu’il existe une détermination continue du logarithme de la fonction a(x), s’il existe une fonction ψ continue à valeur réelle sur X telle que.
Théorème 3.5
Soient X un espace α-connexe, α une application périodique et a(x) 6 = 0 pour tout x. S’il existe une détermination continue du logarithme de la fonction a, alors l’opérateur aT α se transforme en un opérateur à coefficient constant si et seulement si, il est algébrique.
Remarquons que généralement on examine les représentations linéaires de groupes dans l’espace hilbertien. Mais dans le cas des groupes finis, les principaux éléments de la théorie des représentations ont un caractère algébrique propre et sont vrais dans le cas des représentions dans les espaces de Banach, en particulier, pour les représentations linéaires dans l’espace C (X ).
Le groupe commutatif fini Zm possède m représentations irréductibles ρ j , ces représentations sont unidimensionnelles et agissent selon la forme :
Obstacles topologiques de la réductibilité
La condition, utilisée dans le théorème (3.5), d’existence d’une détermination continue du logarithme n’est pas nécessaire. Montrons sur un exemple que cette condition est essentielle.
conclusion
Au cours de cette thèse, nous avons prouvé le lien étroit qui existe entre les propriétés spectrales des opérateurs de déplacement avec poids et les équations cohomologiques . De certaines conditions d’inversibilité de cette classe d’opérateurs, basées sur l’application α et aussi de la dynamique de cette application, nous avons montré une condition suffisante pour qu’une équation cohomologique soit solvable, ou encore soit normalement solvable ; celui-ci repose sur des propriétés spectrales fines de l’opérateur considéré. C’est pourquoi, nous avons établi au préalable, des résultats spectraux concernant un shift bilatéral pondéré sur l’espace séparable et de dimension infinie, qui ont permis d’appliquer le critère de solvabilité des équations cohomologiques, pour une certaine classe de fonctions ayant exactement deux points fixes ou de points selles.
Nous avons considéré naturellement les classes d’applications α à dynamique simple, celles dont les points fixes sont en nombre fini et dont la trajectoire de chacun de ces points converge vers un point fixe. Ces points étant appelés points attractifs , répulsifs ou de points selles.
Il a été montré que la caractéristique dynamique de l’application α utile pour l’obtention des solutions de l’équation cohomologique s’est avérée être un graphe orienté Gα , décrivant la dynamique de l’application α, la plus simple est par exemple que, s’il existe seulement deux points fixes alors le graphe Gα a la forme : F1 → F2.
L’introduction du graphe, a permis d’obtenir une formulation simple des propriétés importantes des opérateurs de composition pondérée.
En utilisant le coefficient a et le nombre λ, on forme deux sous-ensembles de l’ensemble des sommets du graphe. Ces deux sous ensembles forment une partition et donnent une décomposition de graphe sous une certaine condition.
Vu les résultats obtenus dans ce travail, peut-on se demander si de telles conclusions, ou de conclusions similaires peuvent être observées dans les espaces fonctionnels de Hölder, sur une certaine classe d’opérateurs générés par des applications non inversibles incluant les endomorphismes d’algèbre commutative de Banach ; de chercher à mener l’investigation sur d’autres propriétés subtiles relatives aux solutions individuelles des équations fonctionnelles et en particulier à celles appelées équations cohomologiques, voire la connexion entre équations fonctionnelles et équations différentielles fonctionnelles.
Résumé
L’objectif de cette thèse est de donner un certain nombre de résultats relatifs aux propriétés spectrales d’une certaine classe d’opérateurs dits opérateurs de déplacement avec poids c’est-à-dire des opérateurs de forme. En ce qui concerne de tels opérateurs, on se pose beaucoup de questions sur leur comportement spectral et en particulier sur le rapport entre « la dynamique de l’application α et les propriétés spectrales »de ces opérateurs associés à cette application. Ici, une condition suffisante de la solvabilité de l’équation cohomologique basée sur les propriétés spectrales fines de ces opérateurs a été donnée. Un examen minutieux de la réductibilité des opérateurs à déplacement pondéré aux coefficients continus, engendrés par des applications périodiques, continues, d’un espace topologique compact, séparable X , a été effectué. Nous avons généralisé ce résultat en examinant ces opérateurs dans n’importe quel espace de Banach de fonction sur X où ces opérateurs sont bornés et nous avons fourni une certaine relation entre ladynamique de l’application α et les propriétés spectrales de A.
|
Table des matières
Dédicaces
Remerciements
Notations
Résumé
Résumé
Introduction
1 Résultats Préliminaires
1.1 Décomposition du spectre d’un opérateur
1.2 Spectre d’un opérateur de déplacement
1.3 Rayon spectral d’un opérateur de déplacement
2 Opérateurs de composition pondérée sur L2(X, µ)
2.1 Opérateurs de la forme Tα − λI
2.2 Propriétés spectrales d’un opérateur de déplacement avec poids sur un segment
2.3 Influence des points selles sur les propriétés spectrales
2.3.1 Applications diagonales
2.3.2 Difféomorphisme de type Morse- Smale sur un simplexe
3 Réductibilité des Opérateurs de Composition Pondérée
3.1 Introduction
3.2 Factorisation avec déplacement et équation homologique
3.3 Opérateurs de déplacement pondérés réductibles
3.4 Obstacles topologiques de la réductibilité
3.5 Opérateur engendré par la symétrie du carré
conclusion
Bibliographie